No more BS: Is game theory useful in business?

To-date? Nope, not really. But scientific progress happens every day…
“Economic research” and game theory
I’ve learned in recent months that mentioning “economic research” gives rise to a wide range of topics and preconceived notions from business leaders. Some (and maybe most) think of macroeconomic forecasting, and others of policy analysis. Very few talk about what I feel is (or should be) the bread and butter for business economists – pricing models, market assessments, and transaction due diligence.
In these conversations, I’m intrigued by the number of questions I continue to receive about game theory. As executive teams of large companies think more and more critically about geopolitics, ESG approaches, new regulations, and global issues broadly, strategy professionals are clearly looking for more scientific ways to analyze go-to-market, product selection, reputation, etc.
Countless articles (and even more YT videos!) exist on how game theory can be used for business. Though taken together (and based on a review of dozens of these sources), most struggle to get past a few very basic examples of the “prisoner’s dilemma,” or perhaps of a binary decision between ‘Enter’ and ‘Don’t Enter.’ Economics textbooks at least go a bit further. But the question remains…
In what areas, if any, have these concepts moved from the classroom to the boardroom (or circa 2022, the Zoom conference room)?
When push comes to shove, game theory seems to have had limited success in business to-date.
The basics of game theory
Game theory meaningfully enters the curriculum for most economics students through the field of industrial organization (IO). Initially guided by the principles of perfect competition – where the number of firms in an industry alone determines the level of competition – game theory, paving the way for “oligopoly theory,” established that significant competition can exist even between just a few firms.
The key innovation, according to many, is as follows: a firm in a highly concentrated industry is not indifferent to the activities of other firms. That is, in making any decision, the firm has to consider what others will do in response to its decision (or simultaneously).
There are many great articles out there describing the basics of game theory, though I will still (very briefly) summarize the mechanics here. To start, note that traditional IO economists tend to do their analysis through models describing firm characteristics via a series of cost curves and demand curves…
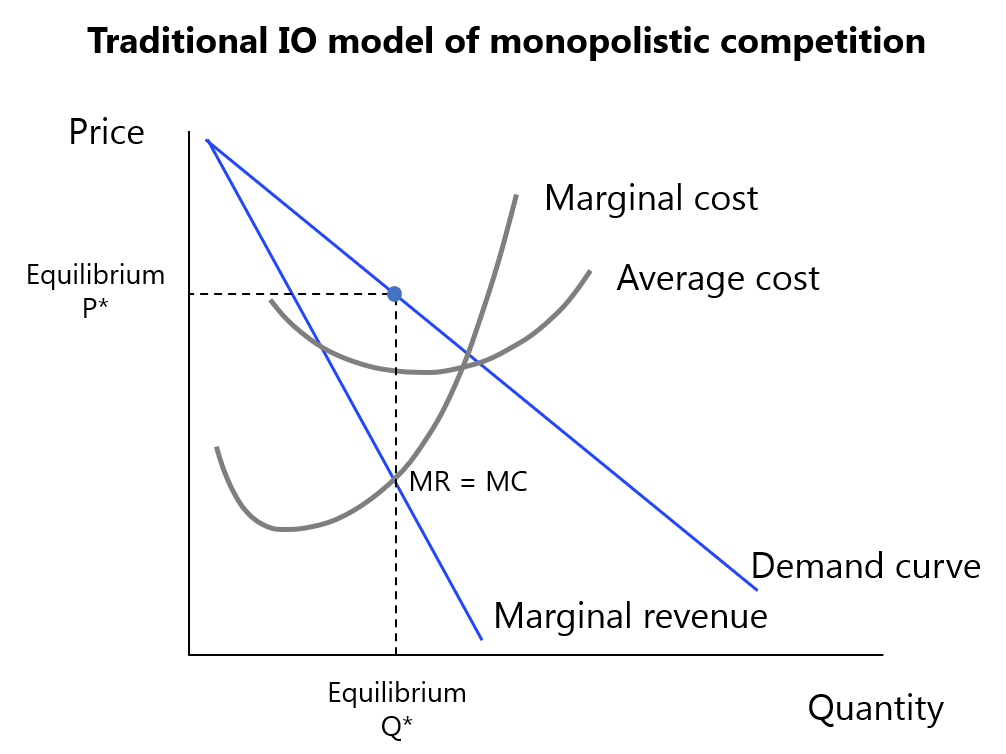
(The above is an illustrative representation of monopolistic competition, a market characterized by product differentiation and few barriers to entry. Equilibrium exists where marginal revenue equals marginal cost. There is no analysis of the interaction between firms; each simply responds to market signals.)
With game theorists, firms are not cogs in a machine. They compete against each other and are faced with clear decisions, each with multiple payoff possibilities depending on the decisions of other firms…
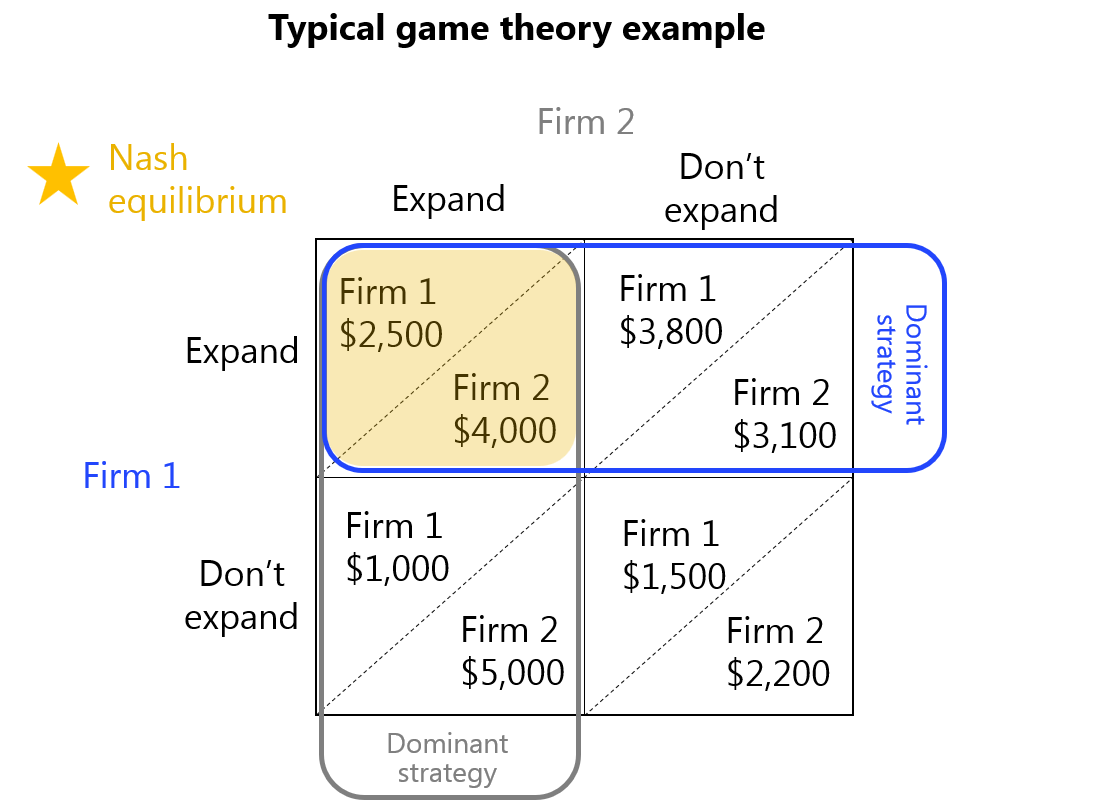
(The above is a typical representation of a game theory problem, where a firm makes a decision based on a competing firm’s decision and the expected payoffs associated with each possibility.)
Firm 1 above makes a decision according to its “dominant strategy,” that is the decision that will maximize payoff regardless of Firm 2’s decision, and vice versa. The intersection of two dominant strategies is a “Nash equilibrium.”
A “prisoner’s dilemma” occurs when the Nash equilibrium exists at a set of decisions that creates a less than optimal outcome for the individuals as a group (remember this one!). This is a widely cited, and seemingly insightful result of game theory analysis.
More complicated games, which I will not describe here, involve multiple sequential decisions, more decision possibilities, and more transformable models, such as the Cournot duopoly model…

(In the above, Firm 1 makes a decision by determining Firm 2’s response to all three of its possible decisions, then selecting the one which results in the highest profit. If Firm 1 undergoes a large expansion, Firm 2’s response will be to not expand, resulting in a sub-game perfect Nash equilibrium.)
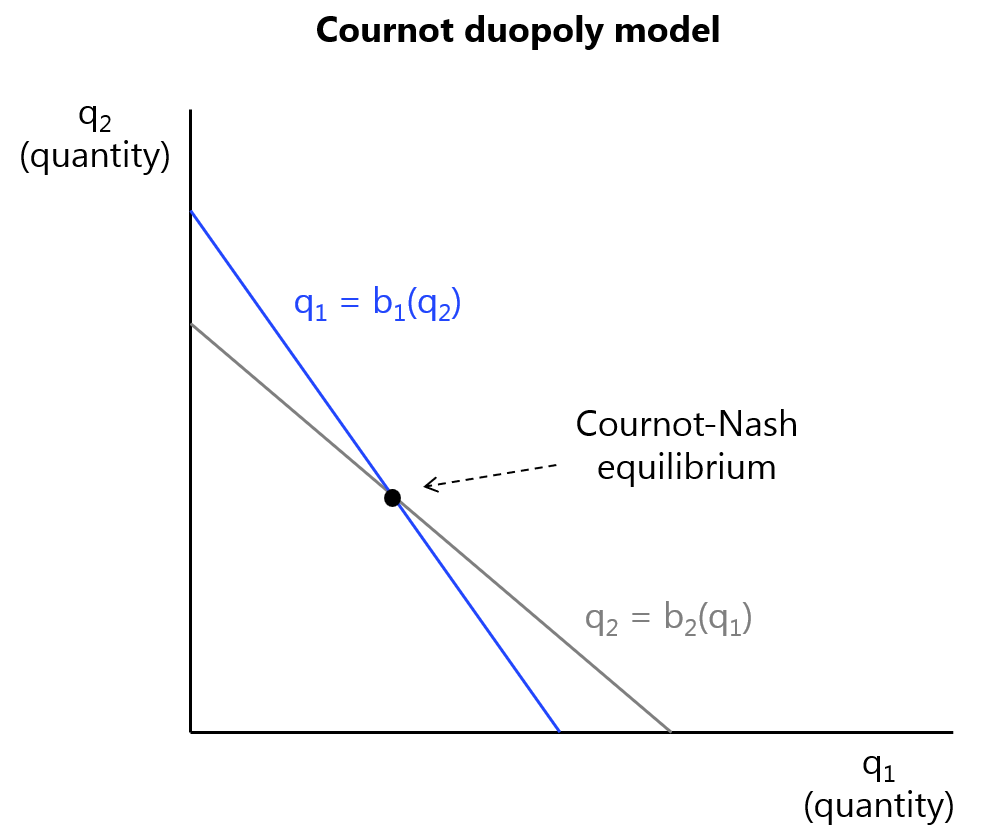
(The Cournot model allows for more comprehensive systems of equations by characterizing firm “response functions.” Firm 1 decides quantity [rather than price] in response to Firm 2’s quantity decision, and vice versa, resulting in a [static] Nash equilibrium.)
These game theory techniques can, according to many, help to improve decision making by modeling strategic interactions in concentrated (rather than “perfectly competitive”) markets. So the goal is simple: make better choices.
Today’s applications of game theory
Search “game theory” in LinkedIn Jobs and a couple hundred results come up. Compare that with the 27K that come up when I type in “benchmarking,” 118K for “scrum,” or even 24K for “regression.” Take it with a grain of salt… clearly, comparisons are hard.
Still, a few common themes arise from the search which provide some limited insight:
- Advanced procurement: Notably as it relates to negotiations, game theory is used to understand the interaction between suppliers and procurement departments including proposing contract terms and pricing considerations. For example, by understanding the Prisoner’s Dilemma, procurement teams can potentially identify new terms of delivery that benefit both parties.
- Antitrust and policy: Public policy is a common use case for game theory. Private companies anticipate antitrust authorities’ reactions to proposed mergers, and use similar tools to anticipate reactions to price changes and new offerings.
- Technology platforms: Generally coupled with auction theory, game theory is used to analyze decisions to expand into new offerings, pricing considerations, and information sharing. For example, new content is consumed and commented on by users based on its valuation to them and their abilities to add new information, up until the point of a Nash equilibrium. This category, and software development in general, is without doubt where game theory is used most significantly in business operations.
Taken together nonetheless, many organizations publish whitepapers about game theory but seeing a BAU process, or even a strategic review, meaningfully incorporating formal game theory models is rare. Even in the above examples (job postings), knowledge of game theory is often an ancillary skill… a shiny object, at that.
It seems generally (and intuitively) that game theory rises in importance and applicability where the games can be isolated to highly controlled environments (such as social media platforms, with structured communication channels and offerings). More on the ideal conditions for game theory later in this article.
No surprise then, some of the most useful applications of game theory I’ve seen in my career were in research around blockchain platforms. For example, consensus protocols for miners can be viewed as “prisoner’s dilemma problems,” where each miner maximizes profit but at a significant cost. More advanced applications in this field include game theory for the implementation of zero-knowledge proofs and other cryptographic techniques (which I have neither the space, nor the brain power to cover sufficiently here!).
In the field of economic research and academia, game theory is used to support a range of applied IO concepts, such as describing prices, sales practices, market structures, and other situations. Many of my lessons in game theory unfolded in the context of market entry – a large incumbent firm, to discourage new entrants, slashes prices significantly resulting in short-run profit issues, but long-run profit maximization thanks to retaining market power. Economists often visualize this practice of “limit pricing” with traditional IO models…
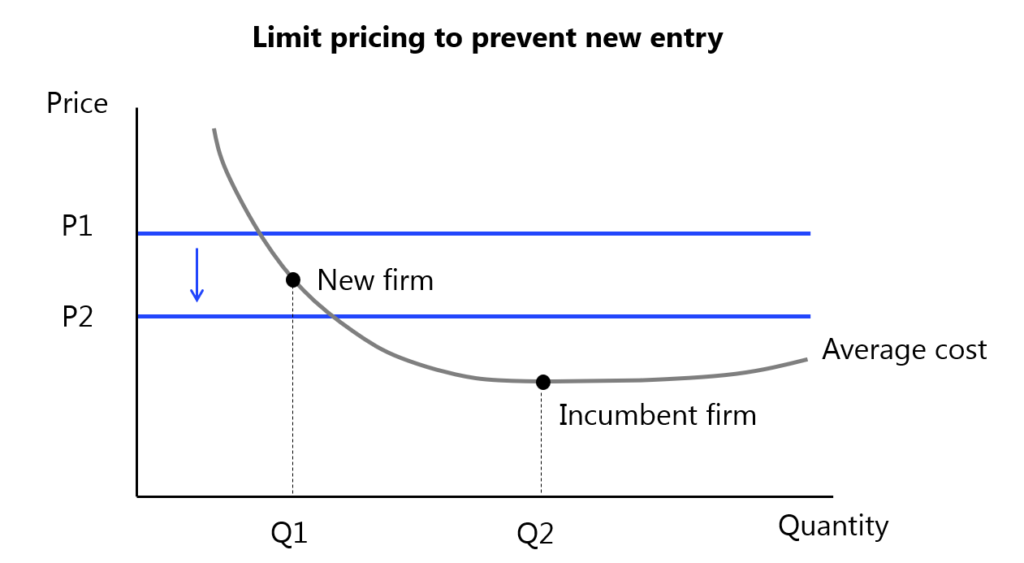
(In the above, the incumbent firm could still charge a higher price for its products [even though below the monopoly price] upon entry, but discounts excessively to prevent entry by the new firm. The new price is below the new firm’s average cost curve and therefore, it will be unprofitable to enter. The above does not include a Nash equilibrium as it is a short run condition.)
Similarly popular examples relate to the incentives of cartel members to renege on an agreed-upon price level.
My own instincts to game theory lessons (in the classroom) were that the models lacked specificity, especially around the rationalities of players. Words like “retaliate,” or “punish” – compared with, say, “maximize” – throw off a subjective feel, compatible with the case study method but not with generalized math models. More on this in the next section, supported by literature.
On the whole, this section, and my own takeaways, can be bluntly summarized (though overexaggerated) with a quote by Ariel Rubinstein, a world-renowned game theorist and NYU professor…

Barriers to adoption
There’s a good reason that the “Game Theory for Business” articles start with 1,000 words summarizing the concept of Nash equilibrium, and 50 words on real business applications…
Spoiler alert, it’s not due to the abstract nature, or restrictive conditions, of game theory models (not entirely, at least). All mathematical economic models require restrictive conditions (for example, many production functions assume only two inputs – capital and labor), yet useful inferences can often still be extracted from these models.
Another spoiler alert, it’s also not (entirely) due to the difficulties of empirically deriving payoff possibilities, though that’s certainly a challenge. Many researchers get around this by using qualitative, relative indicators in payoff matrices (“this decision yields a significantly higher payoff than the alternative”).
The major problems with applied game theory seem to be grounded in a few fundamentals. First, critics argue that too little theory exists behind why the Nash equilibrium is relevant in some scenarios and not relevant in others. Further, critics argue that the Nash equilibrium (and its recent refinements) “use irrationality to arrive at a strong form of rationality” (Aumann 2008). Players in (particularly sequential) games are assumed to be rational, yet what is or isn’t a “rational decision” is often unclear.
On this topic, the individual criticisms are less important. Their significance, and volume, is the problem. The lack of consistency and specificity (mentioned previously) that results has turned game theory into a one-size-fits-all solution for some, especially in the field of IO. The problem is nicely reflected in the below by Larry Samuelson, Professor of Economics at Yale University…

So even with the knowledge of a game, its players, and payoffs, game theory does not provide a clear enough framework for identifying the actual decisions, or outcomes of a situation. The mechanics are straight-forward, but the assumptions are not.
I will add another (and, for better or worse, proprietary) criticism to this list: many of the seemingly ironclad cases of applied game theory I’ve come across could be developed much more clearly and intuitively using simple price theory. Firms entering markets with higher prices is not “retaliation”… it’s just the Law of Supply.
All of that said – lay out a few competitors, a few decisions, and come up with payoff amounts… ignore the fact that you’re missing a bunch of variables, or that you did months of econometrics work to figure out payoff estimates… now, find the Nash equilibrium.
What does it actually tell you? According to some, the suboptimal set of actions you and your competitors might be taking because of information problems (prisoner’s dilemma); for others, a (potentially overly) subjective way to explain strategic decisions. Or in some cases maybe…
… what centuries-old economic theory could have told us much faster, and with significantly more support behind it.
Going forward
Game theorists have had limited success developing applications for practical use in business… but then again, this problem extends to much of economics (the hypothesis at the heart of our business!). On both counts, and despite the analysis here, I am optimistic that business economists will increasingly apply mathematical economic models, including game theory, into research around supply chain, finance, technology… strategy broadly.
The innovations that will drive applied game theory aren’t found in company PRs and whitepapers. Instead, they’re generally buried in the pages of academic journals.
One bright spot is in research on, broadly, the “cooperative approach.” In short – what makes prisoner’s dilemmas interesting, if they are simply inevitable equilibrium outcomes? One word: contracts. Where the appropriate institutions (and transaction cost conditions) exist, prisoner’s dilemmas can be corrected with agreements, and “cooperative outcomes” can be achieved. Now, time to build some business processes around these concepts!
Other bright spots include new empirical and data-gathering techniques, and agency-based computer modeling techniques. Once again, much like adopting a new technology, adopting these methods will take significant learning and research, with collaboration between team leads and economics professionals.
Economics is in a constant state of discovery. Relax the assumptions of perfect competition, and IO theories around trade and decision-making are all over the place. Game theory; information problems; and transaction cost economics – though very different in methodology, all aim to fill in this enormous gap with as much logic as possible. Each can be made useful, with the appropriate team and in the appropriate contexts.
From this analysis and the review of existing applications, let’s infer that game theory can be made most useful where, all else equal:
- You operate in a highly concentrated industry
- You are charged with designing a platform, or with setting up rules to facilitate transactions
- You are engaged in a negotiation that involves just a few participants
- You are engaged in a situation that involves just a few, binary decisions
- You have access to plenty of structured transaction data (for calculating payoffs)
Last but not least… you have the appetite for some exciting R&D work!
…
Significant credit due here to these excellent economists/ authors and pieces of literature, among others:
Ralph Sonenshine | American University | Sourced Economics | The OG Business Economist
Bernard Guerrien | l’Université Paris | “On the current state of game theory.”
Larry Samuelson | Yale University | “Game Theory in Economics and Beyond.”
Ariel Rubinstein | New York University | “How game theory will solve the problems of the Euro Bloc and stop Iranian nukes.”
Robert Aumann | Nobel Prize Winner | Hebrew University of Jerusalem | “Game theory.”
